Скользящее среднее относится к классу индикаторов, следующих за трендом. Оно помогает определить начало новой тенденции и её завершение, по его углу наклона можно определить силу (скорость движения), оно же в качестве основы (сглаживающего фактора) применяется в других технических индикаторах. Иногда скользящее среднее называют линией тренда. Различают три вида средних скользящих линий:
- - простое (Simple Moving Average, SMA)
- - экспоненциальное (Exponential Moving Average, EMA)
- - взвешенное (Weighted Moving Average, WMA)
Для расчета любого вида скользящих средних нужно определенное количество прошлых значений. Как только поступает новое знаечение, из расчета нужно сразу исключить самое старое значение, а вместо него подставлять самое новое (сегодняшнее), чтобы рассчитать текущее среднее скользящее. Получается, что на графике эти скользящие средние «скользят» по оси дат вместе со значениями.
Простое скользящее среднее является обычным арифметическим средним от значений за определенный период.
Формула простого скользящего среднего:

где: Pi - значения (например, цены на рынке) n - длина сглаживания (количество значений, входящих в расчет скользящего)
Экспоненциальное скользящее среднее уменьшает лаг, придавая больший вес последним значениям по сравнению с более дальними значениями. Этот позволяет значительно более быстро реагировать на текущие изменения значения по сравнению с простой скользящей средней. Вес, придаваемый последнему значению, зависит от периода скользящей средней. Чем короче период EMA, тем больший вес будет придаваться последнему значению. Формула простого экспоненциального среднего: Exponential Moving Average = EMA[k-1, n]+(2/(n+1))*(P-EMA[k-1, n]) где: EMA[k, n] — экспоненциальное скользящее среднее периода n на момент k P — текущее значение
Взвешенное скользящее среднее является модификацией простого скользящего среднего с весами подобранными так, что последние значения имеют в средней больший вес. Формула взвешенного скользящего среднего:
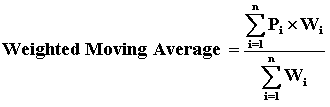
где: Pi - значения i-периодов назад, (i сегодня =1) Wi - веса для значений i-периодов назад
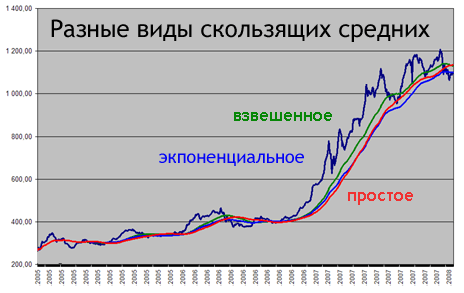
Разница между тремя видами скользящих средних невелика. Среднескользящие линии изменяют свое расположение относительно значений и относительно друг друга в зависимости от динамики значений. Невооруженным глазом видно, что простое среднее скользящее - самое "ленивое", экспоненциальное - самое динамическое. В самом конце графика, когда значения начали снижаться, простое и взвешенное скользящие средние держались на уровне, в то время, как экспоненциальное среднее скользящее быстрее всего приблизилось к значению. Считается, что, на коротких отрезках лучше использовать экспоненциальное среднее скользящее, а на длинных - простое.
Но вернемся к простому скользящему среднему и внимательнее всмотримся в график - мы увидим, что для SMA наблюдается эффект запаздывания при изменении оригинальных значений.
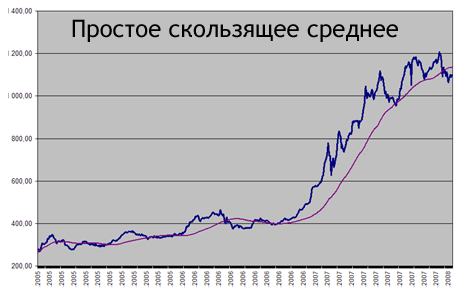
Запаздывание происходит потому, что в расчет среднего принимались только предыдущие значения. А что если в расчет среднего брать одинаковое количество значениий (например, три) из "прошлого" и "будущего", корректно обрабатывая начало и конец отрезка значений?
Как видно из рисунка для:
16.11.2009 SMA = $725 384 = остаток просроченного основного долга; 17.11.2009 SMA = ($725 384 + $720 817 +$703 797) / (1 +1 +1)= $716 666, где 1+1+1 – это 1 день до 17.11.2009, собственно 17.11.2009, 1 день после 17.11.2009; 19.11.2009 SMA = $4 905 776 / (3+1+3) = $700 825, где $4 905 776 – сумма остатков в период с 16.11.2009 по 22.11.2009, (3+1+3) – это 3 дня до 19.11.2009, собственно 19.11.2009, 3 дня после 19.11.2009 3 - выбранное значение из вспомогательного измерения "_Числовые параметры", т.е. "скользить" по трём отчетным дням.
В продолжение предыдущей статьи "SSAS показатели, зависимые от параметров" в MDX-скрипте куба определим следующие меры:
---------------------------------------------------------------------------------------------------------------------------- -- вспомогательная мера для простого скользящего среднего по датам CREATE MEMBER CURRENTCUBE.[MEASURES].[for_SMA] AS MY_ASSP.MinLongInt( COUNT( NONEMPTY( ParallelPeriod([Отчетные даты].[Год-квартал-месяц-дата].[Отчетная дата] ,IIF([_Числовые параметры].[Параметр].CURRENTMEMBER IS [_Числовые параметры].[Параметр].[Не указан], 2, [_Числовые параметры].[Параметр].CURRENTMEMBER.Name ) ) : [Отчетные даты].[Год-квартал-месяц-дата], [MEASURES].[selected_measure] ) ) ,COUNT( NONEMPTY( [Отчетные даты].[Год-квартал-месяц-дата] : ParallelPeriod([Отчетные даты].[Год-квартал-месяц-дата].[Отчетная дата], -1*IIF([_Числовые параметры].[Параметр].CURRENTMEMBER IS [_Числовые параметры].[Параметр].[Не указан], 2, [_Числовые параметры].[Параметр].CURRENTMEMBER.Name ) ,[MEASURES].[selected_measure] ) ) ) - 1 ,VISIBLE = 0 ; -- MY_ASSP.MinLongInt - внешняя хранимая процедура, возвращающая наименьшее значение из двух целочисленных -- вспомогательная мера для простого скользящего среднего по месяцам CREATE MEMBER CURRENTCUBE.[MEASURES].[for_SMAm] AS MY_ASSP.MinLongInt( COUNT( NONEMPTY( ParallelPeriod([Отчетные даты].[Год-квартал-месяц-дата].[Год месяц] ,IIF([_Числовые параметры].[Параметр].CURRENTMEMBER IS [_Числовые параметры].[Параметр].[Не указан], 2, [_Числовые параметры].[Параметр].CURRENTMEMBER.Name ) ) : [Отчетные даты].[Год-квартал-месяц-дата], [MEASURES].[selected_measure] ) ) ,COUNT( NONEMPTY([Отчетные даты].[Год-квартал-месяц-дата] : ParallelPeriod([Отчетные даты].[Год-квартал-месяц-дата].[Год месяц] ,-1*IIF([_Числовые параметры].[Параметр].CURRENTMEMBER IS [_Числовые параметры].[Параметр].[Не указан], 2, [_Числовые параметры].[Параметр].CURRENTMEMBER.Name ) ) ,[MEASURES].[selected_measure] ) ) ) - 1 ,VISIBLE = 0 ; CREATE MEMBER CURRENTCUBE.[MEASURES].[По датам простое скользящее среднее...] AS ( SUM( [Отчетные даты].[Год-квартал-месяц-дата],[MEASURES].[selected_measure] ) +IIF([MEASURES].[for_SMA]<1, NULL, SUM( ParallelPeriod([Отчетные даты].[Год-квартал-месяц-дата].[Отчетная дата], [MEASURES].[for_SMA] ) : [Отчетные даты].[Год-квартал-месяц-дата].PrevMember ,[MEASURES].[selected_measure] ) + SUM( [Отчетные даты].[Год-квартал-месяц-дата].NextMember : ParallelPeriod([Отчетные даты].[Год-квартал-месяц-дата].[Отчетная дата], -1*[MEASURES].[for_SMA] ) ,[MEASURES].[selected_measure] ) ) ) / ([MEASURES].[for_SMA]*2+1) ,FORMAT_STRING = [MEASURES].[selected_measure_format_string] ,ASSOCIATED_MEASURE_GROUP = 'Показатели зависимые от параметров' ,DISPLAY_FOLDER = 'Среднее\Скользящее среднее' ,VISIBLE = 1 ; CREATE MEMBER CURRENTCUBE.[MEASURES].[По месяцам простое скользящее среднее...] AS ( SUM( [Отчетные даты].[Год-квартал-месяц-дата],[MEASURES].[selected_measure] ) +IIF([MEASURES].[for_SMAm]<1, NULL, SUM( ParallelPeriod([Отчетные даты].[Год-квартал-месяц-дата].[Год месяц], [MEASURES].[for_SMAm] ) : [Отчетные даты].[Год-квартал-месяц-дата].PrevMember ,[MEASURES].[selected_measure] ) + SUM( [Отчетные даты].[Год-квартал-месяц-дата].NextMember : ParallelPeriod([Отчетные даты].[Год-квартал-месяц-дата].[Год месяц], -1*[MEASURES].[for_SMAm] ) ,[MEASURES].[selected_measure] ) ) ) / ([MEASURES].[for_SMAm]*2+1) ,FORMAT_STRING = [MEASURES].[selected_measure_format_string] ,ASSOCIATED_MEASURE_GROUP = 'Показатели зависимые от параметров' ,DISPLAY_FOLDER = 'Среднее\Скользящее среднее' ,VISIBLE = 1 ; ----------------------------------------------------------------------------------------------------------------------------
Разместив вспомогательные измерения "_Список показателей", "_Числовые параметры" в область фильтров, определяем простое скользящее среднее для показателя, определяемого выбранным элементом в измерении "_Список показателей", т. е. "сглаживаем"; показатель по величине, устанавливаемой параметром из "_Числовые параметры". Например, мы создали график динамики (см. рисунок выше) суммы остатков просроченного основного долга по договорам розничного кредитования в течение ноября-декабря 2009г. и "сглаживаем" график, используя простое скользящее среднее по трём дням.
Теперь даже самые обычные пользователи кубов легко смогут строить линии трендов на графиках.